Rumus layang layang – Mari kita selami dunia rumus layang-layang, sebuah perjalanan yang akan membuka mata terhadap keindahan matematika yang seringkali tersembunyi di sekitar kita. Layang-layang, dengan bentuknya yang khas dan memukau, bukan hanya sekadar mainan anak-anak, tetapi juga merupakan representasi sempurna dari prinsip-prinsip geometri yang elegan. Memahami rumus layang-layang membuka pintu ke pemahaman yang lebih dalam tentang luas, keliling, dan hubungan sudut-sudut dalam bangun datar yang menarik ini.
Dalam eksplorasi ini, kita akan membongkar definisi layang-layang, menyingkap rumus luas dan kelilingnya, serta melihat bagaimana konsep-konsep ini diterapkan dalam berbagai aspek kehidupan. Kita akan menjelajahi aplikasi praktisnya dalam arsitektur, desain, dan bahkan perhitungan luas lahan. Bersiaplah untuk terpukau oleh keajaiban matematika yang tersembunyi di balik bentuk layang-layang yang sederhana namun mempesona.
Mengungkap Misteri Geometri: Rumus Layang Layang
Mari kita selami dunia geometri yang menakjubkan, khususnya pada bangun datar yang sering kita jumpai: layang-layang. Bangun ini bukan hanya sekadar bentuk yang menghiasi langit saat kita bermain, tetapi juga menyimpan rahasia matematika yang menarik untuk dipecahkan. Kita akan memulai perjalanan ini dengan menggali definisi layang-layang yang komprehensif, menjelajahi ciri-ciri uniknya, dan melihat bagaimana ia berinteraksi dengan bangun datar lainnya dalam perspektif yang lebih luas.
Definisi Layang-Layang yang Komprehensif
Layang-layang adalah bangun datar dua dimensi yang memiliki empat sisi. Keunikan utamanya terletak pada pasangan sisi yang sama panjang. Lebih tepatnya, layang-layang memiliki dua pasang sisi yang sama panjang, di mana setiap pasang sisi bertemu di satu titik sudut. Kedua diagonal pada layang-layang berpotongan tegak lurus, dan salah satu diagonal membagi diagonal lainnya menjadi dua bagian yang sama panjang. Sudut-sudut yang dibentuk oleh sisi-sisi yang tidak sama panjangnya (sudut yang berhadapan) memiliki besar yang sama.
Ciri khas lain yang membedakan layang-layang adalah simetri lipatnya. Layang-layang memiliki satu sumbu simetri, yaitu diagonal yang membagi layang-layang menjadi dua bagian yang kongruen (sama persis). Sumbu simetri ini juga merupakan garis yang membagi sudut yang dibentuk oleh sisi-sisi yang sama panjang menjadi dua bagian yang sama besar. Perlu diingat, meskipun memiliki beberapa kesamaan dengan bangun datar lain, kombinasi karakteristik ini yang membuat layang-layang unik dan mudah dikenali.
Bayangkan sebuah layang-layang yang terbuat dari empat bilah bambu. Dua bilah yang lebih pendek bertemu di satu titik, membentuk sisi-sisi yang sama panjang. Dua bilah yang lebih panjang juga bertemu di satu titik, membentuk sisi-sisi yang sama panjang lainnya. Ketika keempat bilah ini dihubungkan, terbentuklah bentuk layang-layang yang khas. Diagonal-diagonal yang ditarik dari sudut-sudut layang-layang akan berpotongan tegak lurus, dan salah satunya akan membagi diagonal lainnya menjadi dua bagian yang sama panjang.
Ilustrasi Elemen-Elemen Layang-Layang
Mari kita gambarkan layang-layang secara visual. Visualisasi ini akan membantu kita memahami proporsi dan hubungan antar elemennya.
Gambaran deskriptif: Bayangkan sebuah layang-layang berwarna cerah, misalnya merah dan kuning. Layang-layang ini memiliki dua pasang sisi yang berbeda panjangnya. Sisi-sisi yang lebih pendek (misalnya, sisi merah) bertemu di puncak layang-layang, membentuk sudut yang lebih kecil. Sisi-sisi yang lebih panjang (misalnya, sisi kuning) bertemu di bagian bawah layang-layang, membentuk sudut yang lebih besar. Diagonal utama, yang membelah layang-layang menjadi dua bagian simetris, memanjang dari sudut atas ke sudut bawah.
Diagonal lainnya, yang lebih pendek, memotong diagonal utama di tengah, membentuk sudut siku-siku (90 derajat). Perhatikan bagaimana proporsi sisi-sisi dan diagonal menciptakan keseimbangan visual yang khas pada layang-layang.
Ilustrasi ini menunjukkan bahwa:
- Sisi: Terdapat dua pasang sisi yang sama panjang.
- Diagonal: Dua garis yang berpotongan tegak lurus.
- Sudut: Terdapat dua pasang sudut yang sama besar.
Perbandingan Layang-Layang dengan Bangun Datar Lain
Layang-layang memiliki beberapa kemiripan dengan bangun datar lain, namun perbedaan mendasarnya sangat signifikan. Mari kita bandingkan layang-layang dengan belah ketupat dan trapesium untuk melihat perbedaan utama.
Belah Ketupat: Keduanya memiliki empat sisi. Namun, belah ketupat memiliki semua sisi yang sama panjang, sedangkan layang-layang hanya memiliki dua pasang sisi yang sama panjang. Diagonal belah ketupat juga berpotongan tegak lurus dan membagi sudut-sudutnya menjadi dua bagian yang sama besar, sama seperti layang-layang. Perbedaan utama terletak pada panjang sisi dan sifat sudutnya.
Trapesium: Trapesium hanya memiliki sepasang sisi yang sejajar, sementara layang-layang tidak memiliki sisi yang sejajar. Beberapa trapesium khusus (misalnya, trapesium sama kaki) memiliki sifat simetri tertentu, tetapi secara umum, sifat-sifatnya berbeda dari layang-layang. Perbedaan utama terletak pada jumlah sisi sejajar dan sifat sudutnya.
Perbandingan Singkat:
| Fitur | Layang-Layang | Belah Ketupat | Trapesium |
|---|---|---|---|
| Sisi | Dua pasang sisi sama panjang | Semua sisi sama panjang | Sepasang sisi sejajar |
| Diagonal | Berpotongan tegak lurus, satu membagi lainnya | Berpotongan tegak lurus, membagi sudut | Tidak selalu berpotongan tegak lurus |
| Sudut | Dua pasang sudut sama besar | Dua pasang sudut sama besar | Tidak ada sudut yang pasti |
Layang-Layang dalam Kehidupan Sehari-hari
Layang-layang, dengan bentuknya yang khas, dapat ditemukan dalam berbagai aspek kehidupan kita, bahkan di luar permainan anak-anak. Berikut adalah beberapa contoh konkret:
- Desain Arsitektur: Beberapa elemen arsitektur modern mengadopsi bentuk layang-layang. Misalnya, jendela atau atap pada bangunan tertentu dapat dirancang dalam bentuk layang-layang untuk memberikan estetika visual yang unik dan memaksimalkan pencahayaan alami.
- Perhiasan: Bentuk layang-layang sering digunakan dalam desain perhiasan, seperti anting-anting, liontin, atau cincin. Desain ini memberikan kesan elegan dan menarik, serta dapat melambangkan kebebasan dan kreativitas.
- Logo dan Branding: Banyak perusahaan atau merek menggunakan bentuk layang-layang dalam logo mereka. Bentuk ini dapat menyampaikan kesan dinamis, inovatif, dan berorientasi ke depan. Contohnya, beberapa logo perusahaan teknologi atau desain menggunakan bentuk layang-layang yang dimodifikasi.
Kehadiran layang-layang dalam berbagai aspek kehidupan ini menunjukkan betapa bentuk geometris sederhana ini dapat menginspirasi kreativitas dan memberikan dampak visual yang signifikan.
Membongkar Rahasia Rumus Luas
Layang-layang, dengan bentuknya yang unik dan memukau, bukan hanya sekadar hiasan di langit. Di balik keindahannya, tersembunyi prinsip-prinsip geometri yang menarik untuk diungkap. Memahami cara menghitung luas layang-layang membuka pintu ke dunia matematika yang lebih luas, memberikan kita kemampuan untuk memecahkan masalah praktis dan mengapresiasi keindahan bentuk ini dari sudut pandang yang berbeda.
Mari kita selami rahasia di balik perhitungan luas layang-layang, mulai dari rumus dasar hingga metode alternatif yang lebih kreatif.
Membongkar Rahasia Rumus Luas: Lebih dari Sekadar Diagonal
Rumus luas layang-layang dengan menggunakan diagonal adalah cara paling umum dan efisien untuk menghitung luasnya. Rumus ini didasarkan pada dua diagonal layang-layang yang saling berpotongan tegak lurus. Mari kita jabarkan langkah-langkahnya:
- Identifikasi Diagonal: Layang-layang memiliki dua diagonal. Diagonal pertama (d1) adalah garis yang menghubungkan dua titik sudut yang berlawanan, misalnya, titik A ke C. Diagonal kedua (d2) adalah garis yang menghubungkan dua titik sudut lainnya, misalnya, titik B ke D.
- Ukur Panjang Diagonal: Ukur panjang masing-masing diagonal. Gunakan penggaris atau alat ukur lainnya untuk mendapatkan nilai yang akurat.
- Gunakan Rumus: Rumus untuk menghitung luas layang-layang adalah:
Luas = 1/2
- d1
- d2
- Hitung Luas: Kalikan panjang kedua diagonal, lalu bagi hasilnya dengan dua. Hasilnya adalah luas layang-layang.
Contoh Soal: Misalkan sebuah layang-layang memiliki diagonal d1 = 10 cm dan d2 = 8 cm. Maka:
- Luas = 1/2
- 10 cm
- 8 cm
- Luas = 1/2 – 80 cm²
- Luas = 40 cm²
Jadi, luas layang-layang tersebut adalah 40 cm².
Menghitung Luas Layang-Layang Tanpa Diagonal
Selain menggunakan diagonal, ada cara lain untuk menghitung luas layang-layang, yaitu dengan memecahnya menjadi dua segitiga. Metode ini memanfaatkan fakta bahwa layang-layang terdiri dari dua segitiga yang kongruen (sama persis) yang berbagi sisi alas yang sama. Berikut langkah-langkahnya:
- Identifikasi Segitiga: Layang-layang dapat dibagi menjadi dua segitiga dengan menarik garis diagonal yang lebih pendek.
- Ukur Alas dan Tinggi: Ukur panjang alas (sisi diagonal yang lebih pendek) dan tinggi masing-masing segitiga. Perlu diingat, tinggi segitiga adalah garis tegak lurus dari titik sudut ke alas.
- Hitung Luas Segitiga: Hitung luas masing-masing segitiga menggunakan rumus luas segitiga: Luas = 1/2
- alas
- tinggi.
- Jumlahkan Luas: Jumlahkan luas kedua segitiga untuk mendapatkan luas total layang-layang.
Metode ini sangat berguna jika panjang diagonal sulit diukur secara langsung, tetapi ukuran sisi dan tinggi segitiga lebih mudah diakses.
Perbandingan Metode Perhitungan Luas Layang-Layang
Berikut adalah tabel yang membandingkan berbagai metode perhitungan luas layang-layang, beserta kelebihan dan kekurangannya:
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Menggunakan Diagonal |
|
|
| Membagi Menjadi Segitiga |
|
|
Penerapan Praktis Rumus Luas Layang-Layang
Mari kita lihat bagaimana rumus luas layang-layang dapat digunakan dalam kehidupan sehari-hari. Misalnya, Anda ingin membuat layang-layang dengan bentuk yang Anda sukai. Anda dapat menghitung luas permukaan layang-layang yang akan dibuat. Dengan mengetahui ukuran diagonal layang-layang yang Anda inginkan, Anda dapat menghitung luasnya menggunakan rumus 1/2
– d1
– d2. Setelah mengetahui luasnya, Anda dapat memperkirakan jumlah bahan yang dibutuhkan untuk membuat layang-layang tersebut.
Hal ini sangat berguna dalam perencanaan proyek kerajinan tangan, dekorasi, atau bahkan dalam bidang arsitektur untuk desain tertentu.
Rumus Layang-Layang: Lebih dari Sekadar Luas
Layang-layang, bentuk geometris yang memukau mata, lebih dari sekadar permainan di udara. Di balik keindahannya, tersembunyi berbagai perhitungan yang menarik untuk diungkap. Memahami rumus-rumus yang berkaitan dengan layang-layang membuka wawasan tentang dunia geometri, sekaligus mengasah kemampuan berpikir logis dan analitis. Mari kita selami lebih dalam untuk mengungkap rahasia di balik bentuk yang unik ini.
Pemahaman mendalam tentang layang-layang bukan hanya tentang menghitung luas, tetapi juga tentang menguasai perhitungan keliling dan hubungan antar sudutnya. Dengan memahami konsep-konsep ini, kita akan melihat betapa eratnya keterkaitan antara matematika dan dunia di sekitar kita. Mari kita mulai petualangan matematika yang menyenangkan!
Menghitung Keliling Layang-Layang
Keliling layang-layang adalah jumlah total panjang sisi-sisinya. Karena layang-layang memiliki dua pasang sisi yang sama panjang, perhitungan kelilingnya menjadi sangat sederhana. Mari kita pahami langkah-langkahnya melalui contoh berikut:
Misalkan sebuah layang-layang memiliki sisi AB = 10 cm, sisi BC = 15 cm, sisi CD = 10 cm, dan sisi DA = 15 cm. Untuk menghitung kelilingnya, kita cukup menjumlahkan panjang semua sisinya:
- Identifikasi Panjang Sisi: Dalam contoh ini, kita sudah diberikan panjang setiap sisi.
- Rumus Keliling: Keliling (K) = AB + BC + CD + DA
- Substitusi Nilai: K = 10 cm + 15 cm + 10 cm + 15 cm
- Hitung: K = 50 cm
Jadi, keliling layang-layang tersebut adalah 50 cm. Perhatikan bahwa kita juga bisa menggunakan rumus yang lebih singkat, yaitu: K = 2(sisi pendek) + 2(sisi panjang). Dalam contoh di atas, K = 2(10 cm) + 2(15 cm) = 50 cm. Dengan demikian, kita dapat menghitung keliling layang-layang dengan mudah, asalkan kita mengetahui panjang sisi-sisinya.
Contoh Soal Tambahan: Sebuah layang-layang memiliki sisi yang berukuran 8 cm dan 12 cm. Berapakah keliling layang-layang tersebut? Jawab: K = 2(8 cm) + 2(12 cm) = 16 cm + 24 cm = 40 cm.
Hubungan Sudut-Sudut dalam Layang-Layang
Sudut-sudut dalam layang-layang memiliki hubungan yang unik dan menarik. Memahami hubungan ini sangat penting untuk menyelesaikan berbagai soal geometri yang berkaitan dengan layang-layang. Berikut adalah beberapa poin penting yang perlu diperhatikan:
- Jumlah Sudut: Jumlah semua sudut dalam layang-layang adalah 360 derajat, sama seperti pada bangun datar segiempat lainnya.
- Sudut yang Berhadapan: Layang-layang memiliki sepasang sudut yang berhadapan yang sama besar. Sudut yang terbentuk oleh perpotongan diagonal yang lebih pendek akan selalu lebih kecil dibandingkan sudut yang terbentuk oleh perpotongan diagonal yang lebih panjang.
- Diagonal dan Sudut: Diagonal layang-layang berpotongan tegak lurus. Diagonal yang lebih panjang membagi dua sudut yang dibentuk oleh diagonal yang lebih pendek.
Perhatikan ilustrasi berikut untuk memperjelas hubungan sudut-sudut dalam layang-layang:
Misalkan layang-layang ABCD memiliki sudut A dan C yang sama besar. Diagonal AC membagi dua sudut B dan D. Diagonal BD membagi sudut A dan C. Diagonal AC dan BD berpotongan tegak lurus di titik E.
Diagram:
Buatlah sebuah diagram sederhana layang-layang ABCD.
- Tandai sudut A, B, C, dan D.
- Gambarkan diagonal AC dan BD yang berpotongan di titik E.
- Tandai sudut-sudut yang sama besar dengan simbol yang sama (misalnya, garis lengkung tunggal untuk sudut A dan C).
- Tandai sudut-sudut siku-siku (90 derajat) di titik E.
Keterangan:
- Sudut A = Sudut C
- Sudut B + Sudut D = 360 derajat – (Sudut A + Sudut C)
- Diagonal AC membagi dua sudut B dan D.
- Diagonal BD membagi sudut A dan C.
- Sudut AEB = Sudut BEC = Sudut CED = Sudut DEA = 90 derajat
Contoh Soal Gabungan: Keliling dan Sudut
Mari kita selesaikan sebuah contoh soal yang menggabungkan perhitungan keliling dan sudut layang-layang. Contoh soal ini akan menguji pemahaman kita tentang kedua konsep tersebut.
Guys, bayangin deh, betapa kerennya kalau kita bisa melihat dampak positif keragaman budaya di indonesia adalah sebagai kekuatan super yang menyatukan kita. Bukan cuma itu, memahami majas satire adalah kunci untuk membaca dunia dengan lebih tajam, kan? Kita juga harus ingat, mengapa dalam masyarakat yang memiliki keberagaman diperlukan harmoni itu penting banget, demi masa depan yang lebih baik.
Jangan lupa, semangat juang kita seperti dalam syair garuda putih harus terus membara!
Soal: Sebuah layang-layang ABCD memiliki panjang sisi AB = 8 cm, BC = 15 cm, dan sudut A = 100 derajat. Hitunglah:
- Keliling layang-layang.
- Besar sudut C.
Penyelesaian:
- Menghitung Keliling:
- Identifikasi Panjang Sisi: Kita tahu AB = 8 cm dan BC = 15 cm. Karena layang-layang memiliki dua pasang sisi yang sama panjang, maka CD = AB = 8 cm, dan DA = BC = 15 cm.
- Rumus Keliling: K = AB + BC + CD + DA atau K = 2(AB) + 2(BC)
- Substitusi Nilai: K = 8 cm + 15 cm + 8 cm + 15 cm = 2(8 cm) + 2(15 cm)
- Hitung: K = 46 cm
- Menghitung Sudut C:
- Sifat Sudut Layang-Layang: Sudut A = Sudut C
- Substitusi Nilai: Sudut C = 100 derajat
Jawaban:
- Keliling layang-layang adalah 46 cm.
- Besar sudut C adalah 100 derajat.
Dengan menyelesaikan soal ini, kita telah menggabungkan pengetahuan tentang keliling dan sudut layang-layang. Ini menunjukkan betapa pentingnya memahami konsep-konsep geometri secara menyeluruh.
Aplikasi Praktis
Rumus layang-layang, lebih dari sekadar konsep matematika di buku pelajaran, memiliki peran penting dalam dunia nyata. Penerapannya luas, mulai dari perencanaan arsitektur hingga perhitungan luas lahan. Mari kita bedah bagaimana rumus sederhana ini membuka pintu menuju solusi praktis dan efisien.
Penerapan Rumus Layang-Layang dalam Arsitektur dan Desain
Dalam dunia arsitektur dan desain, rumus layang-layang menjadi alat bantu yang tak ternilai. Bentuk layang-layang, dengan keunikan simetri dan proporsinya, seringkali menjadi inspirasi dalam menciptakan elemen estetis dan fungsional. Penerapan ini tidak hanya mempercantik tampilan, tetapi juga memberikan solusi struktural yang cerdas.
Sebagai contoh, perhatikan desain atap bangunan. Atap berbentuk layang-layang, misalnya, dapat memaksimalkan efisiensi penggunaan material dan distribusi beban. Dengan memahami rumus luas layang-layang, arsitek dapat menghitung luas permukaan atap dengan tepat, memastikan kestabilan struktur dan efisiensi biaya.
Selain atap, elemen desain seperti jendela, pintu, atau bahkan fasad bangunan dapat mengadopsi bentuk layang-layang. Desainer dapat memanfaatkan rumus untuk menentukan ukuran dan proporsi yang ideal, menciptakan tampilan yang menarik dan unik. Bayangkan sebuah bangunan dengan jendela-jendela berbentuk layang-layang yang artistik, memberikan kesan dinamis dan modern. Penggunaan rumus memastikan presisi dalam perencanaan dan eksekusi desain.
Sebagai contoh visual, kita bisa membayangkan sebuah bangunan museum dengan atap berbentuk layang-layang yang lebar. Atap ini tidak hanya berfungsi sebagai pelindung, tetapi juga sebagai elemen estetis yang memukau. Dengan menggunakan rumus luas layang-layang, arsitek dapat menghitung luas atap, mempertimbangkan faktor-faktor seperti sudut kemiringan dan kebutuhan pencahayaan alami. Hasilnya adalah bangunan yang indah, fungsional, dan efisien.
Penerapan dalam Perhitungan Luas Lahan dan Area
Rumus layang-layang juga memiliki aplikasi penting dalam perhitungan luas lahan atau area yang memiliki bentuk menyerupai layang-layang. Dalam bidang pertanian, pertambangan, atau bahkan perencanaan kota, kemampuan untuk menghitung luas area secara akurat sangat krusial.
Sebagai contoh kasus, bayangkan seorang petani yang memiliki sebidang lahan berbentuk layang-layang. Petani tersebut perlu mengetahui luas lahan untuk menghitung kebutuhan bibit, pupuk, atau bahkan potensi hasil panen. Dengan mengukur panjang diagonal-diagonal layang-layang, petani dapat dengan mudah menghitung luas lahan menggunakan rumus:
Luas = ½ × d1 × d2
di mana d1 dan d2 adalah panjang diagonal-diagonal layang-layang. Dengan perhitungan yang tepat, petani dapat membuat keputusan yang lebih baik dalam pengelolaan lahan dan meningkatkan efisiensi pertanian.
Dalam perencanaan kota, rumus layang-layang juga dapat digunakan untuk menghitung luas area taman, lapangan, atau fasilitas publik lainnya yang memiliki bentuk layang-layang. Perhitungan yang akurat membantu dalam perencanaan anggaran, penataan ruang, dan evaluasi efektivitas penggunaan lahan.
Sebagai contoh, sebuah pemerintah kota berencana membangun taman bermain anak-anak dengan bentuk layang-layang. Dengan mengukur diagonal-diagonal taman, pemerintah dapat menghitung luas area taman dan merencanakan fasilitas yang sesuai, seperti area bermain, jalur pejalan kaki, dan area hijau. Penggunaan rumus memastikan perencanaan yang efisien dan pemanfaatan lahan yang optimal.
Kuis Pemahaman Rumus Layang-Layang
Uji pemahaman Anda tentang rumus layang-layang dengan kuis singkat berikut:
- Sebuah layang-layang memiliki diagonal-diagonal dengan panjang 12 cm dan 16 cm. Berapakah luas layang-layang tersebut?
- Jika luas sebuah layang-layang adalah 60 cm², dan salah satu diagonalnya berukuran 10 cm, berapakah panjang diagonal yang lain?
- Sebuah layang-layang memiliki luas 48 cm². Jika panjang salah satu diagonal adalah dua kali panjang diagonal lainnya, berapakah panjang kedua diagonal tersebut?
Kunci Jawaban dan Penjelasan:
- Luas = ½ × 12 cm × 16 cm = 96 cm². Rumus luas layang-layang: ½ × d1 × d2
- 60 cm² = ½ × 10 cm × d2. Maka, d2 = (60 cm² × 2) / 10 cm = 12 cm.
- Misalkan d1 = x dan d2 = 2x. Maka, 48 cm² = ½ × x × 2x, atau 48 cm² = x². Dengan demikian, x = √48 = 4√3 cm. Jadi, diagonal-diagonalnya adalah 4√3 cm dan 8√3 cm.
Skenario: Membuat Layang-Layang Raksasa
Bayangkan Anda ditugaskan untuk membuat layang-layang raksasa untuk festival layang-layang di kota Anda. Layang-layang tersebut harus memiliki bentuk layang-layang dengan panjang diagonal 6 meter dan 8 meter. Berapakah luas permukaan layang-layang tersebut? Jika Anda membutuhkan 1 meter persegi bahan untuk setiap layang-layang, berapa banyak bahan yang Anda butuhkan?
Solusi:
Luas layang-layang = ½ × 6 meter × 8 meter = 24 meter persegi. Jadi, Anda membutuhkan 24 meter persegi bahan untuk membuat layang-layang raksasa tersebut.
Mari kita telaah bersama, betapa indahnya negeri ini. Dampak positif keragaman budaya di Indonesia adalah seperti permata yang tak ternilai, memperkaya khazanah kita. Memang, hidup ini tak selalu mudah, tapi dengan pemahaman, kita bisa melihat sisi humor, seperti saat kita belajar majas satire adalah cermin bagi realita. Kita butuh harmoni. Oleh karena itu, mengapa dalam masyarakat yang memiliki keberagaman diperlukan harmoni , jawabannya jelas: untuk keindahan bersama.
Semangat ini tercermin dalam syair garuda putih , sebuah simbol yang menginspirasi.
Eksplorasi Lanjutan
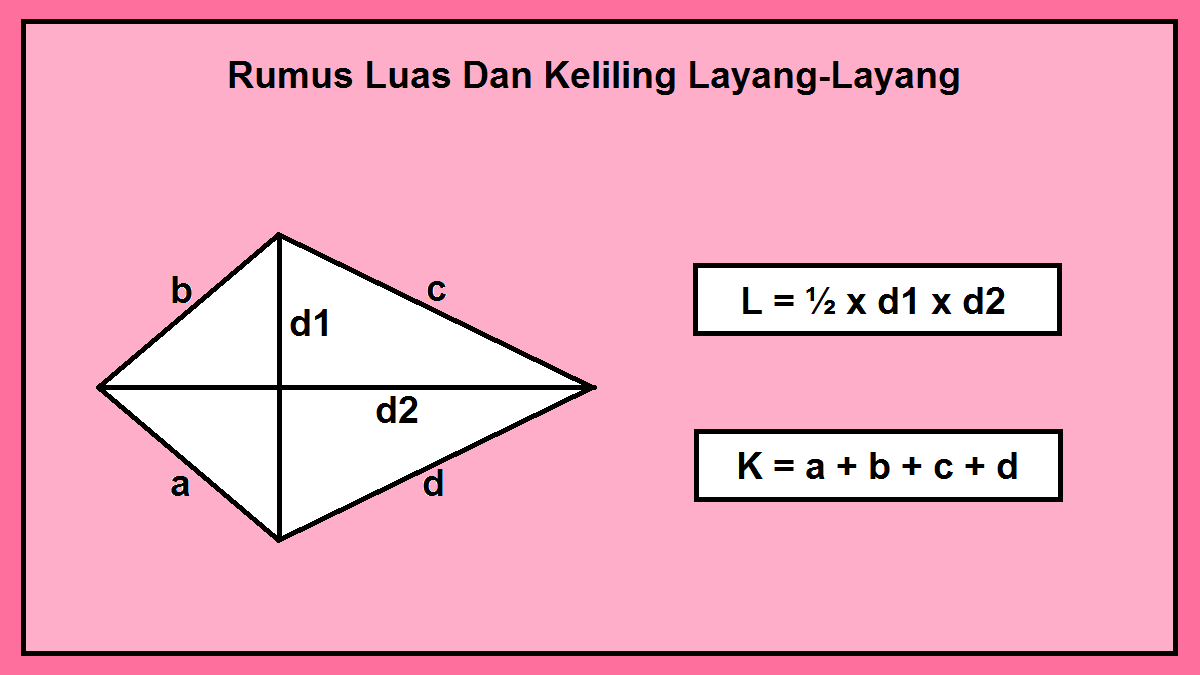
Source: cilacapklik.com
Mari kita selami lebih dalam dunia layang-layang! Setelah memahami dasar-dasarnya, kini saatnya kita menjelajahi bagaimana rumus luas layang-layang bisa menjadi lebih fleksibel dan bermanfaat. Kita akan melihat bagaimana rumus ini dapat dimodifikasi, diaplikasikan dalam berbagai situasi, serta tantangan apa saja yang mungkin muncul.
Kita akan membahas variasi rumus, contoh penerapan, dan bahkan kutipan dari sumber terpercaya untuk memperkuat pemahaman kita. Tujuannya adalah untuk membuka wawasan tentang betapa luasnya aplikasi konsep geometri ini.
Modifikasi dan Adaptasi Rumus Layang-Layang
Rumus luas layang-layang, yang kita tahu adalah 1/2
– d1
– d2 (dengan d1 dan d2 adalah panjang diagonal), ternyata memiliki fleksibilitas yang luar biasa. Kita bisa mengadaptasinya untuk menghitung luas bangun datar yang “mirip” layang-layang, bahkan ketika bentuknya tidak sempurna simetris. Kuncinya adalah mengidentifikasi elemen-elemen kunci yang relevan.
Sebagai contoh, pertimbangkan sebuah bangun datar yang menyerupai layang-layang tetapi memiliki sisi-sisi yang tidak sama panjang. Kita tetap bisa menggunakan prinsip dasar rumus luas layang-layang. Pertama, kita harus mengidentifikasi diagonal utama bangun tersebut. Kemudian, kita ukur panjang diagonal tersebut. Jika bangun tersebut dapat dibagi menjadi dua segitiga, kita dapat menghitung luas masing-masing segitiga (1/2
– alas
– tinggi) dan menjumlahkannya.
Alas dan tinggi segitiga ini akan terkait dengan diagonal dan bagian-bagiannya.
Proses ini memerlukan sedikit kreativitas dan kemampuan visualisasi. Kita harus mampu “melihat” diagonal utama dan membagi bangun menjadi bentuk-bentuk yang lebih sederhana. Pendekatan ini memungkinkan kita untuk menghitung luas bangun yang kompleks dengan menggunakan prinsip-prinsip dasar geometri.
Variasi Rumus Luas dan Keliling
Rumus dasar luas layang-layang dapat dimodifikasi untuk menghitung luas dengan cara yang berbeda, tergantung pada informasi yang tersedia. Selain itu, kita juga akan melihat bagaimana menghitung keliling layang-layang.
- Menggunakan Sudut dan Sisi: Jika kita mengetahui panjang sisi-sisi layang-layang dan salah satu sudut antara sisi-sisi tersebut, kita dapat menggunakan trigonometri untuk menghitung luas. Misalnya, jika kita memiliki dua sisi yang berdekatan (a dan b) dan sudut antara keduanya (θ), luasnya dapat dihitung dengan rumus: Luas = a
– b
– sin(θ). - Keliling Layang-Layang: Keliling layang-layang dihitung dengan menjumlahkan panjang keempat sisinya. Karena layang-layang memiliki dua pasang sisi yang sama panjang, rumusnya menjadi: Keliling = 2
– (sisi1 + sisi2). - Contoh Penerapan: Dalam desain arsitektur, rumus luas layang-layang dapat digunakan untuk menghitung luas permukaan atap yang berbentuk layang-layang. Dalam dunia penerbangan, konsep ini bisa diaplikasikan untuk menghitung luas sayap pesawat yang mendekati bentuk layang-layang.
Kutipan Sumber Terpercaya
“Dalam bidang teknik sipil, perhitungan luas layang-layang sering digunakan untuk mengestimasi luas penampang melintang saluran irigasi yang berbentuk menyerupai layang-layang, membantu dalam perencanaan dan pengelolaan sumber daya air.”
– Sumber: Jurnal Teknik Sipil, Universitas Gadjah Mada.
Tantangan dan Solusi dalam Penggunaan Rumus Layang-Layang, Rumus layang layang
Meskipun rumus layang-layang sangat berguna, ada beberapa tantangan yang mungkin muncul dalam penerapannya. Memahami tantangan ini dan solusinya akan meningkatkan kemampuan kita dalam menggunakan konsep ini secara efektif.
- Kesulitan dalam Mengukur Diagonal: Dalam situasi tertentu, seperti saat menghitung luas lahan yang berbentuk mendekati layang-layang, mengukur diagonal secara langsung bisa jadi sulit.
- Solusi: Gunakan metode triangulasi atau pengukuran tidak langsung dengan memanfaatkan sifat-sifat geometri, seperti sudut dan sisi, untuk menghitung panjang diagonal.
- Bentuk yang Tidak Sempurna: Bentuk layang-layang yang tidak simetris sempurna dapat menyulitkan perhitungan.
- Solusi: Bagi bentuk tersebut menjadi beberapa bagian yang lebih sederhana (misalnya, segitiga atau trapesium) dan hitung luas masing-masing bagian, lalu jumlahkan.
- Keterbatasan Informasi: Terkadang, informasi yang tersedia (seperti panjang sisi atau sudut) terbatas.
- Solusi: Gunakan teorema Pythagoras, trigonometri, atau metode estimasi untuk memperkirakan nilai yang hilang berdasarkan informasi yang ada.
Akhir Kata
Dari perhitungan luas hingga penemuan sudut-sudutnya, rumus layang-layang membuka wawasan baru tentang dunia di sekitar kita. Ingatlah bahwa matematika bukanlah sekadar kumpulan angka dan rumus, tetapi juga bahasa yang memungkinkan untuk memahami dan menghargai keindahan alam semesta. Teruslah menjelajahi, bereksperimen, dan jangan pernah berhenti bertanya. Dengan semangat yang membara, setiap orang dapat menguasai konsep-konsep ini dan menemukan keajaiban matematika di mana pun berada.
Jadikan rumus layang-layang sebagai awal dari petualangan matematika yang tak terbatas.